지난 시간 복습, 벡터, 선형 의존과 독립
직선으로는 방향이 표현되지 않는다. 그래서 벡터를 사용하는 것.
일상 생활에서는 distance. 공간도 수학에서는 유클리드 거리라고 한다.
어떤 공간이라도 논리적으로 규명할 수 있는 체계. 우리가 사는 세계는 유클리드, 기하학 공간.
실수에서 하나의 수가 가지고 있는 크기(원점으로부터의 거리)와 방향(+, -)
절대값을 사용하면 원점으로부터의 속성을 가져올 수 있다. 이를 벡터공간에서 사용할 수 있다.
벡터는 체의 성질을 가진 수 (스칼라로 구성된다)
공간에 대한 시스템을 구축하기 위해 필요한 것
1. 벡터와 벡터의 덧셈
2. 벡터와 스칼라의 곱셈
3. 벡터와 벡터의 곱셈
두 개를 더했을 때 영벡터가 나오는 것들은 선형 의존의 관계에 있다.
n개까지 확장이 되는 개념이며, 선형 의존과 선형 독립에 대해 이해해야 한다.
선형대수학은 그래픽스 외로도 빅데이터 등 다양한 분야에서 사용된다.
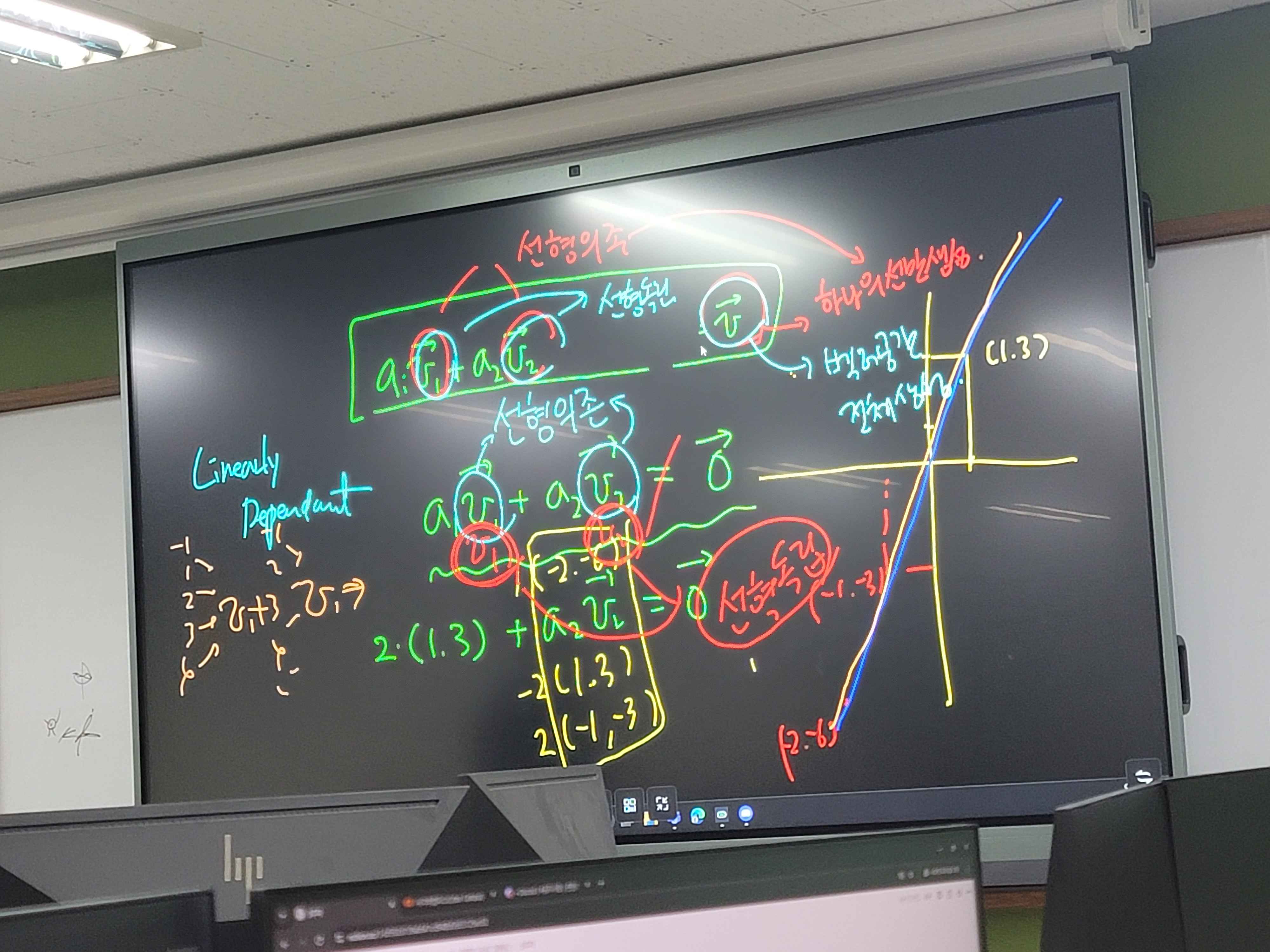
선형 결합 (Linear Combination)
벡터 공간의 두 연산을 사용해 새로운 벡터를 만들어내는 식
선형 의존(Dependent)
모든 a가 0이 아님에도 영벡터를 만들 수 있다면
선형 결합에 사용된 벡터는 선형 의존의 관계를 가짐
선형 독립(Independent)
모든 a가 0이어야만 영벡터를 만들 수 있다면
선형 결합에 사용된 벡터는 선형 독립의 관계를 가짐
기저벡터(Basis Vector)와 차원(Dimension)
- 기저 (Basis) : 벡터 공간의 모든 벡터를 생성할 수 있는 선형 독립의 성질을 가지는 벡터의 집합
- 기저 벡터(Basis Vector) : 기저의 원소
- 표준 기저벡터(Standard Basis Vector) : 한 축만 사용하는 단위 벡터
- 차원(Dimension) : 기저의 수
기저라는 개념은 집합이다.
수업 요약
- 차원이란 무엇인가
- 선형 결합
- 선형 의존 & 선형 독립
- 기저, 기저벡터, 표준기저벡터
- 각, 크기, Norm
과제
[벡터 공간]
- 벡터 공간을 구성하는 선형 결합식에 대해 정리하시오
- 선형 의존과 선형 독립의 정의를 쓰고 이에 대해 설명하시오.
- 선형 의존인 벡터가 가지는 문제에 대해 자신의 생각을 정리하시오
- 2차원 벡터 공간에서 선형 독립과 연립 방정식 풀이의 관계에 대해 자신의 생각을 정리하시오
- 기저, 기저벡터, 표준기저벡터, 차원의 정의를 쓰시고
- 3차원 벡터공간에는 왜 기저벡터가 3개 필요한지 자신의 생각을 정리하시오
[삼각함수]
- 데카르트 좌표계에서의 각의 측정 방법, 삼각형의 피타고라스 정리, 사인, 코사인, 탄젠트에 대해 정리하시오.
- 반지름이 1인 원호 위에 존재하는 벡터 (x, y)에 대응하는 삼각함수 좌표에 대해 대해 정리하시오
- 크기가 r인 벡터 공간 내 임의의 벡터 (x, y)에 대응하는 삼각함수 좌표에 대해 정리하시오
https://se-jeon.notion.site/3-c2c8280842744f80b0591b5ab061a7a1?pvs=4
3주차 과제 | Notion
과제
se-jeon.notion.site
'대학생활 > 수업' 카테고리의 다른 글
| 게임사운드기초 3주차 - 소리의 구성 요소 (0) | 2024.09.12 |
|---|---|
| 게임사운드제작실습 3주차 - 에디터 사용법, 발소리 제작 (0) | 2024.09.12 |
| 게임연출기획 3주차 - 시나리오와 게임 연출 (1) | 2024.09.09 |
| 게임시스템기획포트폴리오 2주차 - 포트폴리오 제작 방향성 (2) | 2024.09.05 |
| 게임사운드기초 2주차 - 사운드의 역할 및 특징 (4) | 2024.09.05 |



