기존에 수업했던 Soft Renderer는 오른손 좌표계이지만, DirectX는 왼손 좌표계이다.
왼손 좌표계
- DirectX, Unity, Unreal
오른손 좌표계
- OpenGL
1학기 때의 내용을 복습
벡터
크기와 방향을 모두 가지고 있는 기하학적 객체
- Position vector (위치 벡터) : 시작점이 원점이며 공간상 한 점이 끝점으로 구성된 벡터
- Unit vector (단위 벡터) : 벡터의 크기가 1인 벡터
- Direction vector (방향 벡터) : 공간상에서 방향을 나타내는 벡터
- Normal vector (법선 벡터) : 평면세 수직인 벡터
- Zero vector (영 벡터) : 벡터의 모든 성분이 0인 벡터
- Inverse vector (역 벡터) : 기존 벡터의 크기는 같으나 방향이 반대 방향인 벡터
벡터 내적 (Dot product)
주어진 두 벡터의 성분들을 곱한 후, 그들의 합, 스칼라 값
a 내적 b = ||a|| ||b|| cosθ = x1x2 + y1y2 + z1z2
벡터 외적 (Cross product)
3차원 공간의 두 벡터의 이항연산으로 새로운 벡터 반환
a 외적 b = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)
|| a x b || = || a || || b || sinθ (0 <= θ <= π)
왼손 좌표계에서 외적은 왼손으로 감는 방향으로 벡터가 생김
벡터 a = (1, 3, 2), b = (2, 4, - 1)일 때에 c = a 내적 b, d = b 내적 a를 계산한 후에 c가 a, b에 대해서 직교임을 확인하고 c, d가 평행인지 확인 해 보려면...
행렬
직사각형 모양으로 행과 열로 수 또는 기호 혹은 다항식을 표현
행렬의 가로 방향을 행(row), 세로 방향(column)
행벡터 (Row vector or Row matrix)
하나의 행으로 구성된 행렬
열벡터 (Column vector or Column matrix)
하나의 열로 구성된 행렬
DirectX 행렬또한 일반적인 행렬과 크게 다르지는 않지만, 차이점이 있다.
정사각행렬 (Square matrix)
행렬의 행과 열의 개수가 같은 행렬
ex : 2*2
전치행렬 (Transpose matrix)
원래 행렬의 행과 열을 서로 바꾼 행렬, 알파벳 T를 이용한다.

단위행렬 (Identity matrix)
행렬의 주대각선 성분들은 1이고 나머지는 0인 정방행렬, 알파벳 I 사용
대각 행렬 (Diagonal matrix)
행렬의 주대각선 성분들은 제외하고 나머지는 0인 정방행렬
영행렬 (Zero matrix or null matrix)
행렬의 모든 성분들이 0인 행렬, 알파벳 O를 주로 사용
행렬식 (Determinant)
역행렬의 존재여부를 확인하는 수식이며, 0이면 역행렬이 존재하지 않는다.
행렬식은 정방행렬(Square matrix)에서만 존재한다.
행렬 A의 행렬식 표기법 : det(A) or | A |
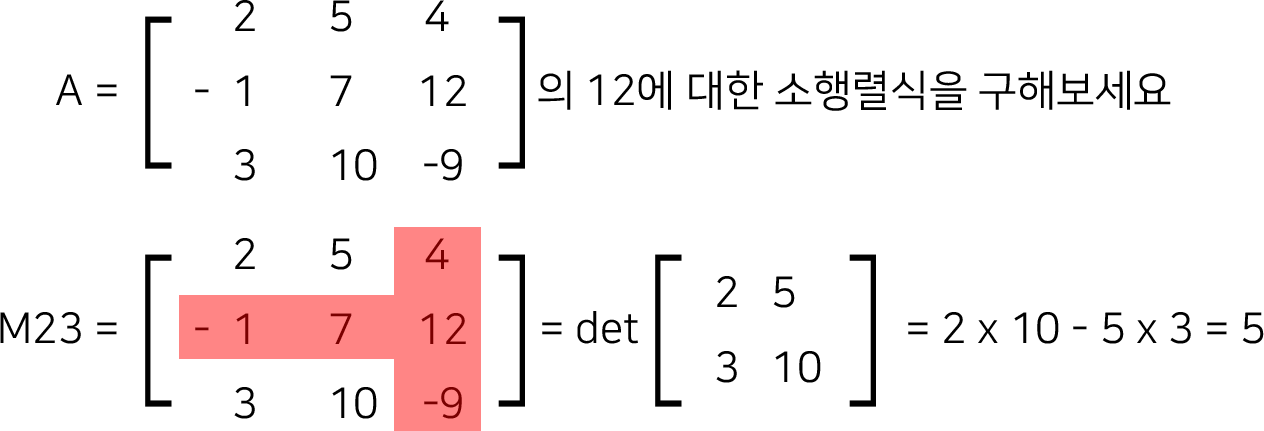
소행렬식 (Minor)
역행렬을 구하기 위해서 행렬식을 구한다.
가장 먼저 Minor, 소행렬식을 알아야 한다.
소행렬식이란?
정사각형 A의 원소 aij에 대한 소행렬식 Mij는 i행과 j열의 모든 원소들을 제거한 후 남은 행렬의 행렬식이다.



여인수 (餘因數, Cofactor)
정사각행렬 A의 원소 aij에 대한 여인수 Cij는 지정된 원소의 자리 부호를 적용한 소행렬식 (Minor)
특정 행 또는 열을 제외하고, 남은 소행렬의 행렬식에 적당한 부호를 붙인 값.
소행렬식을 구하는데, 소행렬식 앞에 부호를 결정하는 부분까지 포함되어 있는 것.
(도저히 이해할 수 없어 찾아봤던 강의, 이 영상 짱 쉽게 설명함.)
https://youtu.be/cq1tM72nkL4?si=A9I8JnUpr3kW8rqT&t=176



Confactor Matrix (여인수 행렬)
정사각행렬 A에 대해서 각 원소 aij에 대한 여인수 cij로 구성된 행렬
Adjoint Matrix (수반 행렬, 딸림 행렬)
A에 대한 여인수 행렬의 전치행렬
행렬식 공식
특정 행을 따라서 구한다. 일반적으로 첫번째 행 진행.
(1:15:00 부근, 무슨 말씀이신지 못 알아들었다.)
Inverse Matrix (역행렬)
- 행렬의 곱셈에 대해서 역원이 역행렬
- 행렬의 모든 성분들이 0인 행렬, 알파벳 O를 주로 사용한다.
- 정사각행렬이고 행렬식이 0이 아닌 행렬만 역행렬이 가능하다.
- 역행렬이 존재하는 행렬을 가역행렬(Invertible matrix)라 함.
기저와 기저벡터
기저 (Basis)
벡터 공간 내 선형독립인 벡터들의 집합
- 선형독립 관계를 가진 벡터들은 벡터 공간안에 독립적인 방향
- 선형종속 관계를 가진 벡터들은 벡터 공간안에 서로 평행
기저벡터 (Basis Vector)
기저에 속해 있는 임의의 벡터.
선형 독립이며, 선형 결합으로 벡터 공간의 모든 벡터 표현 가능
차원 (Dimension)
기저를 구성하고 있는 기저벡터의 개수
- 2차원 평면은 2개의 선형 독립적인 벡터로 구성
- 3차원 평면은 3개의 선형 독립적인 벡터로 구성
표준기저 (Standard Basis)
지정된 차원에 대해 선형 독립인 단위벡터들의 집합
표준기저벡터 (Standard Basis Vector)
표준기저를 구성하고 있는 개별 벡터들
2차원 공간
- 표준기저 : {(1,0), (0,1)}
- 표준기저벡터 : ex = (1,0)0, ey = (0,1)
3차원 공간
- 표준기저 : {(1,0,0), (0,1,0), (0,0,1)}
- 표준기저벡터 : ex = (1,0,0), ey = (0,1,0), ez = (0,0,1)
N차원 공간에서의 표준기저와 표준기저벡터 확장 가능
선형변환
벡터공간 V에서 벡터공간 W 사이의 선형성을 만족하는 함수
벡터에서의 선형성(Linearity)
벡터공간 V에 속한 벡터 u, v에 대해서 가산성(Additivity) 성립
- f(u+v) = f(u) + f(v)
벡터공간 V에 속한 벡터 u, k에 대해서 동차성(Homogeneity) 성립
- f(ku) = kf(x)
행렬과 기저벡터의 관계 (행렬을 행 우선 기준 : 행 우선 행렬, DirectX)
벡터공간 V의 표준기저벡터를 이용해 선형결합으로 모든 벡터를 표현한다.
Row Major Matrix(행 우선 행렬)의 벡터와 행렬 곱셈의 순서 : 벡터 다음에 행렬
크기 변환 행렬 S
회전 변환 행렬 R
- x축 회전 변환 행렬 (Rx)
- y축 회전 변환 행렬 (Ry)
- z축 회전 변환 행렬 (Ry)
아핀변환
선형 변환에 이동 변환의 결합으로 구성된 변환
선형변환은 행렬의 곱셈, 이동변환은 벡터의 덧셈으로 구현 가능.
하나의 행렬로 선형변환과 이동변환을 합친 형태 (y = Ax)
동차좌표계를 이용해야 한다.
동차좌표계 (Homogeneous Coordinate)
기존 차원에서 하나의 차원을 추가해서 표현한 좌표계
3차원 기반 동차좌표계 : 4차원 점 : P(x, y, z, 1), 벡터 : v(x, y, z, 0)
이동 변환 행렬 (T)
동차좌표계를 이용해서 3차원 공간에서는 4x4 행렬로 표현한다.

크기 변환 행렬 (S)
동차좌표계를 이용해서 3차원 공간에서는 4x4 행렬로 표현한다.

회전 변환 행렬 (R)
xyz축의 오일러각을 통한 회전 변환
현재 3D좌표계에서 Roll : z축(r), Pitch : x축(b), Yaw : y축(a)
z축 회전 > x축 회전 > y축 회전
행렬의 순서가 중요하다.

'대학생활 > 수업' 카테고리의 다른 글
| 게임인공지능 2주차 - Design Pattern, 전략 디자인 패턴, 옵저버 패턴, 데코레이터 패턴 (1) | 2023.09.05 |
|---|---|
| 게임밸런스및시뮬레이션 2주차 - 게임 밸런스의 이해 (0) | 2023.09.04 |
| 게임배경음악과효과음 1주차 - OT (0) | 2023.08.31 |
| 게임기획과비주얼스크립팅 1주차 - OT (0) | 2023.08.31 |
| 레벨디자인심화 1주차 - OT (1) | 2023.08.31 |

