[ 4주차 ]
[ 좌표계의 기원과 정의 ]
- 좌표계 : 공간에서 점의 위치를 숫자나 기하학적 요소를 사용해 나타낸 체계
- 고대 그리스에서 기하학을 발전시키면서 좌표계 개념으로 확대
- 고대 그리스 천문학자들의 삼각 측량법이 좌표계의 초기 형태
- 지구에서 관측한 2개 지점 사이 거리와 각도를 통해 별의 위치 추정
- 기하학 > 대수학 > 해석기하학
[ 좌표계의 종류 ]
- 직교좌표계 (데카르트 좌표계)
- 극좌표계
- 구면좌표계
- 원통좌표계
[ 데카르트 좌표계 ]
Cartesian coordinate system
- 좌표평면 : 2D 좌표계, 2차원 평면에서 x축과 y축의 한 쌍으로 표현
- 좌표공간 : 3차원 좌표계, 3차원 평면에서 x축과 y축, z축 한 쌍으로 표현
[ 극좌표계 ]
2D 평면 상의 점의 위치를 원점의 거리와 X축과의 각도를 사용해 점의 위치 표현
- (r, θ)로 위치 표현
- x = r * cos(θ)
- y = r * sin(θ)
[ 방정식의 이해 ]
- 하나 이상의 미지수가 포함된 두 수학적 표현식이 같은 값을 가짐을 나타내는 관계
- 복잡한 형태의 문제를 단순화 시켜서 수학적으로 표현 가능
[ 일차 방정식의 이해 ]
일차 방정식 (Linear equation 혹은 선형방정식)
미지수 최고 차항의 차수가 1인 다항 방정식
- 기하학적으로 직선의 방정식
- 방정식의 해인 (x, y) 2차원 좌표평면에 좌표로 표현 가능
- 좌표평면에 있는 모든 선은 일차 방정식의 해
- 그래프로 표현된 직선은 방정식의 대응을 통해서 표현된 결과
[ 이차 방정식의 이해 ]
이차 방정식 (Quadratic equation)
미지수 최고 차항의 차수가 2인 다항 방정식
- 기하학적으로 포물선 형태
- 포물선은 y축을 기준으로 대칭
[ 이차 방정식과 원 ]
미지수가 3개인 이차 방정식
원을 2차 방식으로 표현, (a, b)는 원점, r은 반지름
원점이 중심이고 r인 방정식
[ Python 기초 ]
환경 설정 방법, 출력 방식, 모듈, 변수, 리스트, 튜플, 연산자, 반복문, 조건문, 함수의 이해.
Pygame 기본 구조 이해. 선 그리기, 좌표 평면 만들기 실습 진행.
[ 5주차 ]
[ 벡터의 정의 ]
벡터 (Vector) : 크기와 방향을 모두 가지고 있는 기하학적 객체
시작점과 끝점을 기준으로 하여 화살표로 표시한다.
크기와 방향이 같은 벡터 v와 벡터 u는 같은 벡터이다.
[ 스칼라의 정의 ]
스칼라 (Scalar) : 크기만을 가진 값. 실수나 정수 형태의 값.
방향이 없어서 온도, 무게, 길이와 같은 특정 크기만 표현한다.
사칙 연산이 가능하다.
[ 벡터와 N차원 ]
N차원에 대해서 벡터는 N개의 성분(Component)을 가진다.
N차원일 경우 벡터의 성분들을 나열한 형태로 표현한다.
[ 벡터의 크기 ]
노름 (norm) : 수학에서 벡터의 길이를 말하며 벡터의 방향과는 독립적이다.
[ 벡터의 연산 ]
- 벡터와 벡터 덧셈 : 시작점을 같게 만드는 것이 중요하다. 교환 법칙이 성립한다.
- 벡터와 벡터 뺄셈 : 벡터의 뺄셈은 역벡터의 덧셈과 같다. 교환 법칙이 성립하지 않는다.
- 벡터와 스칼라 곱셈 : 벡터와의 곱셈은 기존 벡터의 방향과 무관하며 크기만 변경된다.
- 벡터와 스칼라 나눗셈 : 벡터와의 나눗셈은 기존 벡터의 방향과 무관하며 크기만 작게 변경한다.
- 벡터와 스칼라배 : 벡터와 스칼라의 곱셈과 나눗셈은 결국 벡터의 각원소에 스칼라를 곱셈하는 것으로써 벡터의 스칼라배 혹은 스칼라곱셈이라고 칭함.
[ 벡터의 종류 ]
- 위치벡터 (Position vector) : 시작점이 원점이며 공간상 한 점이 끝점으로 구성된 벡터. 공간상의 위치를 벡터로 표현한다.
- 단위벡터 (Unit vector) : 크기가 1인 벡터, 기존 벡터에 벡터의 크기를 나눠서 계산 가능하다.
- 방향벡터 : 공간상에서 방향을 나타내는 벡터. 두 점 사이의 위치를 통해서 방향을 구할 때 사용한다.
- 법선벡터 (Normal vector) : 특정 직선이나 평면에 수직인 벡터.
- 영벡터 (Zero vector) : 벡터의 모든 성분이 0인 벡터. 크기도 0이고 방향이 정해져 있지 않다.
- 역벡터 (Inverse vector) : 기존 벡터의 크기는 같으나 방향이 반대 방향인 벡터. 벡터의 덧셈의 역원은 역벡터.
[ 벡터 공간 ]
벡터 공간 (Vector space) : 벡터들로 구성되어진 집합이며, 공집합이 아니다. 10가지 공리로 구성되어 있다.
- 집합 V에 대해서 벡터 공간의 10가지 공리를 만족할 경우 집합 V를 벡터 공간, 집합 V의 원소를 벡터라고 한다.
01. 두 벡터의 덧셈은 벡터 공간 안에 속한다.
02. 두 벡터의 덧셈은 교환 법칙이 성립한다.
03. 두 벡터의 덧셈은 결합 벅칙이 성립한다.
04. 두 벡터의 덧셈에 대해서 항등원이 존재한다.
05. 두 벡터의 덧셈에 대해서 역원이 존재한다.
06. 벡터와 스칼라의 곱셈은 벡터 공간 안에 속한다.
07. 스칼라들의 곱셈에 대해서 결합법칙이다.
08. 스칼라 덧셈에 대해서 분배 법칙이 성립한다.
09. 두 벡터와 스칼라 k에 대한 분배 법칙이 성립한다.
10. 곱셈에 대한 항등원이 존재한다.
[ 벡터의 생성과 선형 결합 ]
각 항에 상수를 곱하고 결과를 더함으로써 일련의 항으로 구성된 표현식이다.
벡터 v가 벡터의 스칼라배들을 통해 일차식의 합으로 표현된다. 일차 결합이라고도 한다.
벡터 공간에서의 가장 기본적인 연산. 벡터 공간의 합.
벡터들을 스칼라배와 벡터 덧셈을 통해 조합하여 새로운 벡터를 얻는 연산이다.
[ 선형 독립 ]
영벡터가 나오기 위해서 모든 a값이 0이어야 할 때.
모든 벡터가 남은 벡터들의 일차 결합으로 나타낼 수 없는 벡터들의 집합.
서로 같은 직선에 존재하지 않을 때.
[ 선형 종속 ]
모든 a가 0이 아님에도 영벡터를 만들 수 있을 때.
평행해서 선형 결합을 해도 결과가 직선상으로만 나올 때.
[ 기저와 기저벡터 ]
- 기저 (Basis) : 벡터 공간 내 선형독립인 벡터들의 집합
- 기저벡터 (Basis Vector) : 기저에 속해 있는 임의의 벡터. 선형 독립이며, 선형 결합으로 벡터 공간의 모든 벡터를 표현 할 수 있다.
[ 표준 기저와 표준기저벡터 ]
- 차원 (Dimension) : 기저를 구성하고 있는 기저벡터의 개수.
2차원 평면은 2개의 선형 독립적인 벡터로 구성됨.
3차원 평면은 3개의 선형 독립적인 벡터로 구성됨.
- 표준기저 (Standard Basis) : 지정된 차원에 대해 선형 독립인 단위벡터들의 집합.
- 표준기저벡터 (Standard Basis Vector) : 표준기저를 구성하고 있는 개별 벡터들.
ex)
- 2차원 공간에서의 표준기저 : {(1,0), (0,1)}
- 2차원 공간에서의 표준기저벡터 : e1 = (1,0), e2 = (0,1)
- 3차원 공간에서의 표준기저 : {(1,0,0),(0,1,0),(0,0,1)}
- 3차원 공간에서의 표준기저벡터 : e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)
[ 벡터의 내적 ]
- 스칼라곱 (scalar product, dot product or inner product) : 주어진 두 벡터의 성분들을 곱한 후 그들의 합
- 도트(·)를 이용하여 연산기호로 사용한다.
- a·b = x1x2 + y1y2
- 계산 결과는 스칼라 값을 반환한다.
- 내적은 교환 법칙이 성립한다.
- 내적은 분배 법칙이 성립한다.
- 내적은 결합 법칙이 성립하지 않는다. (내적의 결과는 스칼라이므로 스칼라와 벡터는 내적 성립이 불가능)
- 벡터 자신의 내적은 벡터 자신의 크기에 제곱과 동일하다.
- 플레이어의 바라보는 각도를 기준으로 한 상대 객체의 앞뒤를 판정할 수 있다. (정규화 필수)
앞일 경우 내적값 양수, 뒤일경우 내적값 음수, 직각일 경우 내적값 0.
- 플레이어가 바라보는 시야 안에 객체가 들어왔는지 판정할 수 있다.
[ 벡터의 외적 ]
- 벡터곱 (Vector product) or cross product
- 기본적으로 3차원 공간에서 정의한다.
- 크로스(×)를 이용하여 연산기호로 사용한다.
- 계산 결과는 벡터를 반환한다.
- a×b = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)
- 외적은 교환 법칙이 성립하지 않는다.
- 외적은 결합 법칙이 성립하지 않는다.
- 외적은 분배 법칙이 성립한다.
- 플레이어의 바라보는 각도를 기준으로 상대 객체의 좌우를 판정할 수 있다. (정규화 필수)
외적 후 y축 기준벡터와 내적 결과가 양수이면 객체는 왼쪽, 외적 후 y축 기준벡터와 내적 결과가 음수이면 객체는 오른쪽
외적 후 결과가 0이면 객체는 시선방향과 평행
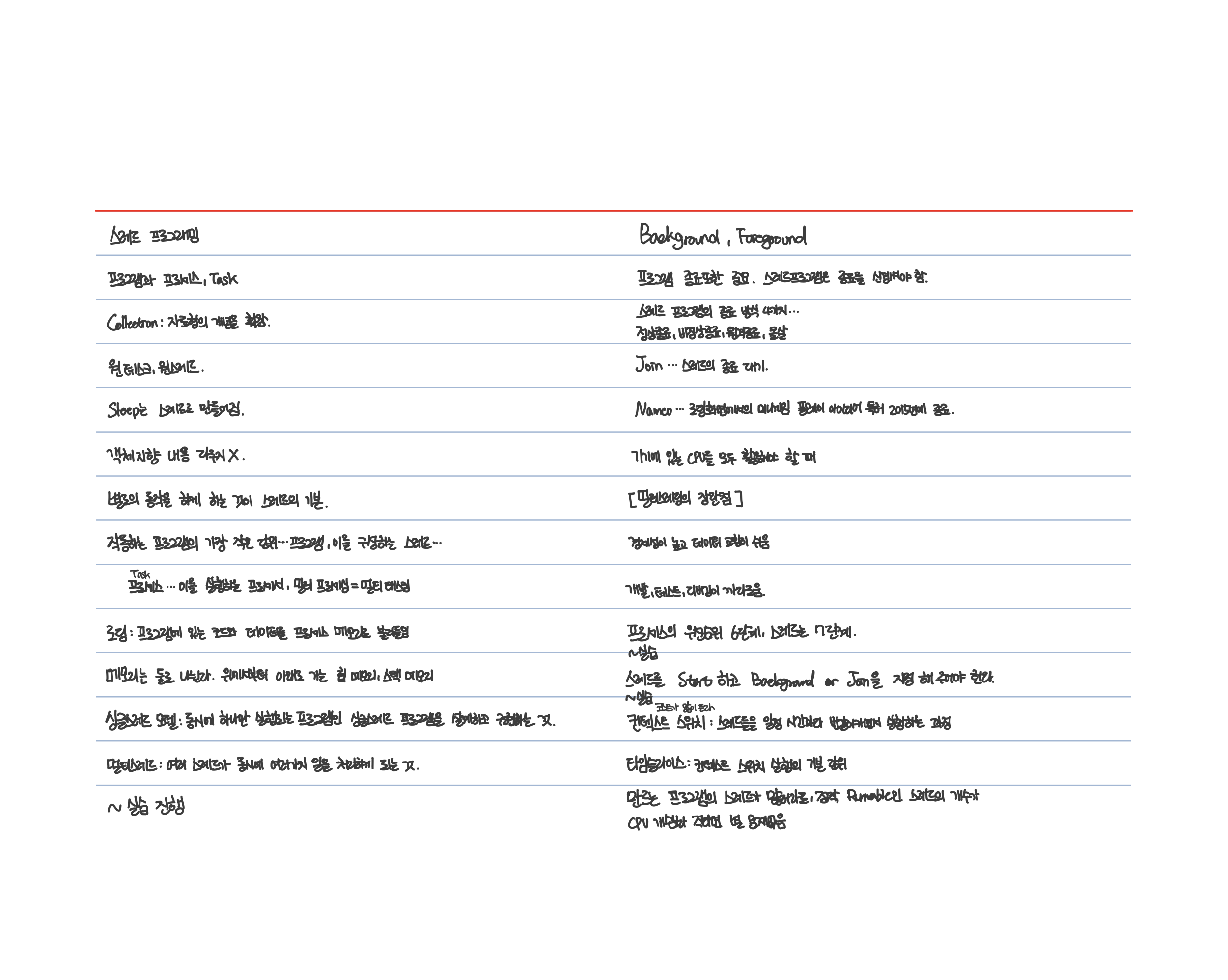


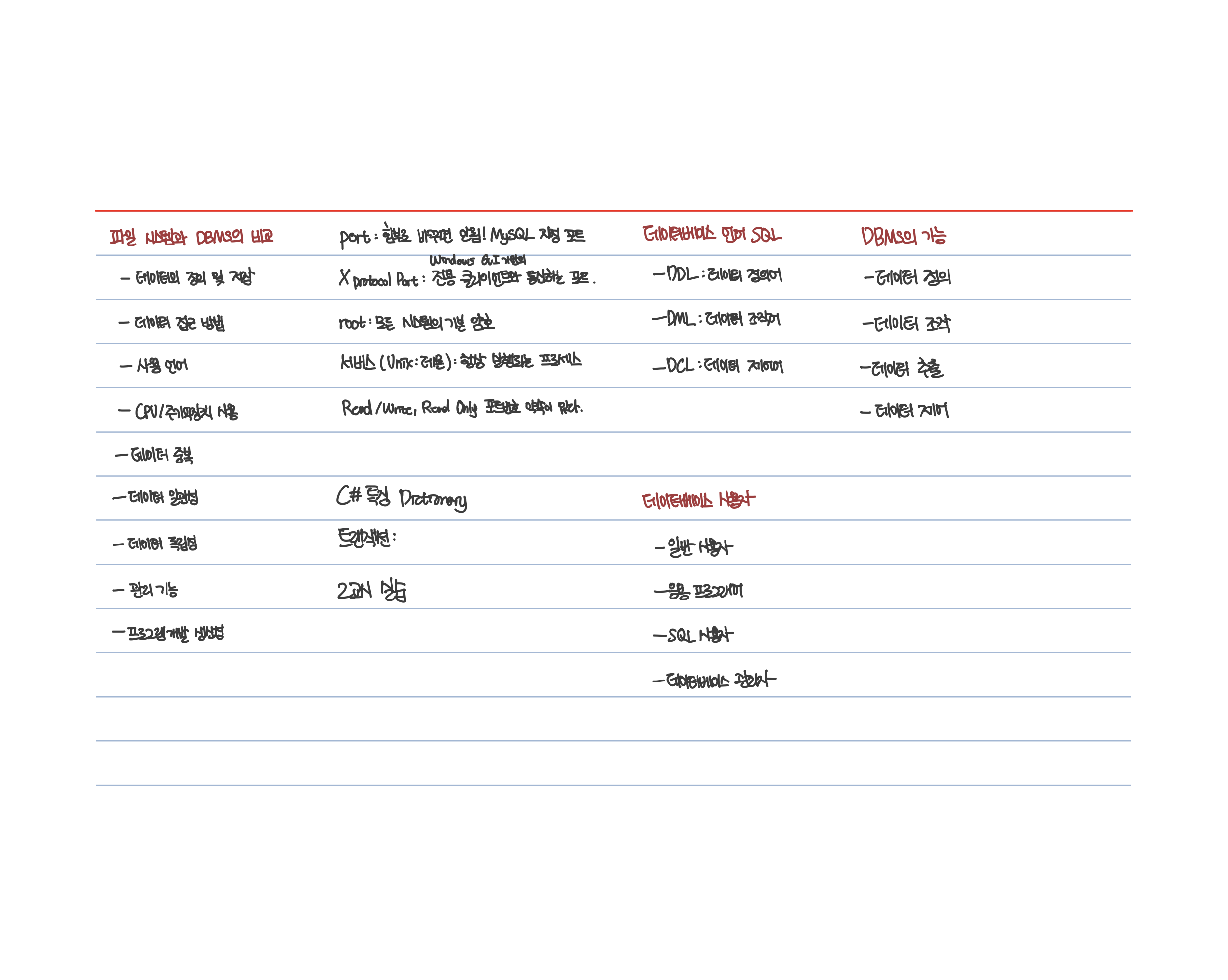

'대학생활 > 수업' 카테고리의 다른 글
| 게임기획크리틱 4~5주차 (0) | 2023.04.12 |
|---|---|
| 게임기획크리틱 2~3주차 (0) | 2023.04.12 |
| 게임그래픽프로그래밍 2~3주차 - 수의 체계, 연산, 각도와 삼각비, 삼각함수 (0) | 2023.04.10 |
| 게임네트워크프로그래밍 4~5주차 (0) | 2023.04.10 |
| 게임네트워크프로그래밍 2~3주차 (0) | 2023.04.10 |

