[ 2주차 ]
[ 수의 명제, 정의, 정리, 공리 ]
명제 (Proposition) : 참 혹은 거짓을 판단할 수 있는 문장이나 식
정의 (Definition) : 추상적인 의미를 명확하게 나타낸다.
정리 (Theorem) : 증명된 수학 이론, 참이 검증된 이론
공리 (Axiom) : 증명 없이 일반적으로 진실이라고 받아들이는 문장이나 이론, 식
[ 유클리드 5개 공준 (Postulate, 기하학적 공리) ]
- 동일한 것과 같은 것들은 서로 같다.
- 같은 것에 어떤 같은 것을 더하면 그 전체는 서로 같다.
유클리드 원론 : 전세계에서 성경 다음으로 많이 읽혀진 책
1. 임의의 점에서 임의의 점으로 직선을 그릴 수 있다.
2. 직선에서 연속적으로 유한한 직선을 만들 수 있다.
3. 임의의 중심과 반지름을 가진 원을 그릴 수 있다.
4. 모든 직각은 서로 같다.
5. 한 선분을 서로 다른 두 직선이 교차할 때, 두 내각의 합이 180보다 작으면,
이 두 직선을 무한히 연장하면 두 내각의 합이 180도 보다 작은 쪽에서 교차한다. (평행선 공준)
[ 수의 체계 ]
- 0 : 인도에서 처음 등장, 개념은 이전 부터 있었다.
- 양의 정수 (자연수)
- 음의 정수
- 정수
- 유리수
- 무리수
- 실수
[ 수의 기본 연산 - 용어 ]
- 기본연산 : 덧셈, 뺼셈, 곱셈, 나눗셈
- 연산자 : 연산을 수행하는 기호
- 피연산자 : 연산에 참여하는 수나 변수
[ 수와 이항연산 ]
- 이항연산 (Binary Operation)
사칙연산은 이항연산의 구조를 띈다.
[ 이항연산의 성질 ]
- 닫힘 성질 (Closure Property) : 연산자와 피연산자가 집합A의 원소일 경우 이항 연산의 결과도 다시 집합 A의 원소가 되는 성질
- 결합 법칙 (Associativity)
- 교환 법칙
- 분배 법칙 : 좌분배 법칙과 우분배 법칙이 모두 성립하면 연산 +에 대한 연산 *는 분배법칙이 성립한다.
- 항등원 : 임의의 수 a에 대해서 연산한 후에 a를 유지하게 만드는 수. (연산 결과가 자기 자신이 되게 만드는 수)
- 역원 : 임의의 수 a에 대해서 연산한 후에 항등원을 만드는 수.
[ 함수의 개요 ]
- 함수 (Function) : 두 개의 집합 X, Y가 있을 때 X에 속한 각 원소들에 대응하는 Y에 속한 원소들이 유일하게 관계가 성립.
- 정의역(domain) : X
- 공역(codomain) : Y
- 함숫값 : X의 원소 x에 대응하는 Y의 원소 y값
- 치역(range) : 함숫값의 집합
[ 함수의 종류 ]
- 단사함수 (Injection, One-to-one) : 정의역 하나의 원소가 공역 하나의 원소에 유일하게 대응, 일대일 관계.
- 전사함수 (Surjection, Onto) : 공역과 치역이 같은 함수.
- 전단사함수 (Bijection) : 정의역과 공역의 원소가 중복없이 일대일로 대응한 함수. 전사함수 + 단사함수.
- 합성함수 : 2개 이상의 함수를 연결하여 하나의 함수를 만드는 것.
- 항등함수 (Identity function) : 정의역과 공역이 동일하고 모든 원소들이 자기자신에 대응하는 함수. 항등원과 동일한 성질을 지닌다. (합성 결과는 원 함수와 동일하다.)
- 역함수 (Inverse function) : 정의역과 치역이 서로 뒤바뀐 값을 얻는 함수. 전단사함수는 역함수가 반드시 존재한다.
[ 3주차 ]
[ 각도의 이해 ]
- 각도 : 2개의 교차하는 직선이나 평면 사이를 측정하는 단위.
- 도 (Degree) : 원의 한 바퀴를 360등분하여 각도를 표현. (각도법)
- 라디안 (Radian) : 호(Arc)의 길이를 통해서 각도를 표현하는 방법. (호도법, 180도 = ㅠ)
- 원주율 (Pi) : 원둘레와 원의 지름의 비율.
- 원하는 각도에 ㅠ/180를 곱하면 원하는 radian을 구할 수 있다.
[ 삼각비 ]
- 삼각비 : 삼각형의 밑변, 빗변, 높이의 길이에 대한 비율
- 피타고라스의 정리 : 밑변의 제곱 + 높이의 제곱 = 빗변의 제곱, 피타고라스의 정리는 밑변, 빗변, 높이 길이들의 관계.
- 삼각비는 직각 삼각형에서만 적용 가능하다.
- 일반 삼각형이여도 언제든지 직각 삼각형으로 계산이 가능하다.
- 사인(sine) : 높이/빗변
- 코사인(cosine) : 밑변/빗변
- 탄젠트(tangent) : 높이/밑변
[ 삼각함수의 정의 ]
- 삼각함수 : 직각삼각형의 각을 두 변의 길이의 비율과 연관시키는 함수.
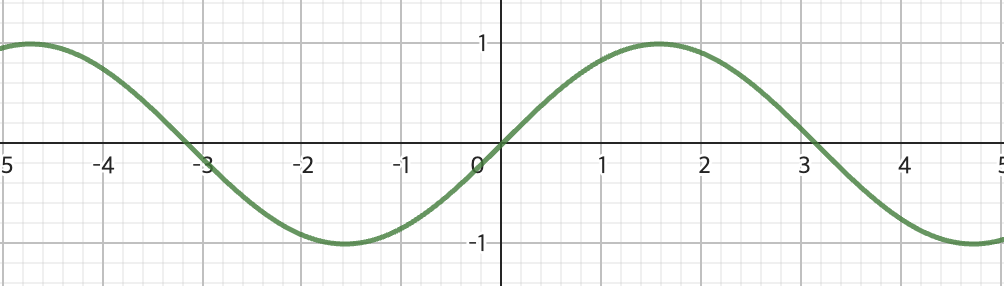
- 사인함수 : x의 범위는 모든 실수, y의 범위는 -1이상 1이하. 주기는 2ㅠ, 원점에 대칭한 형태. odd function.
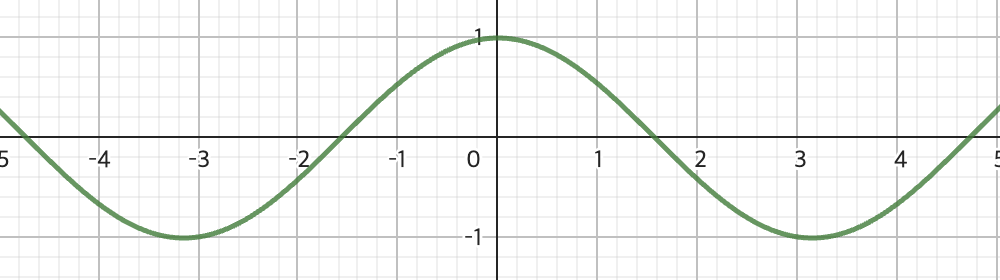
- 코사인함수 : x의 범위는 모든 실수, y의 범위는 -1이상 1이하. 주기는 2ㅠ, y축에 대칭. even function.
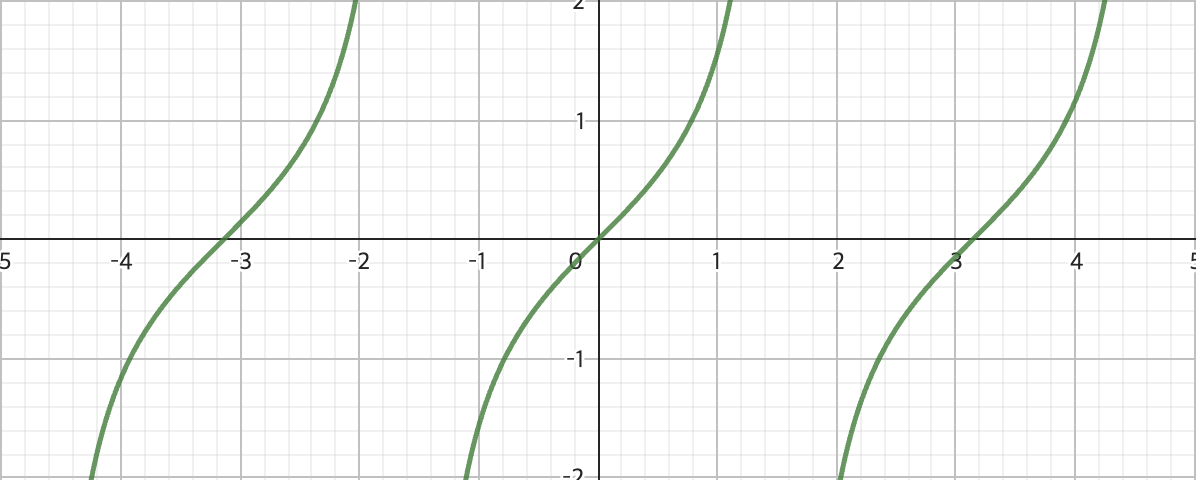
- 탄젠트 함수 : x의 범위는 ㅠ/2 + nㅠ가 아닌 실수, y의 범위는 모든 실수. 주기는 ㅠ, 원점에 대칭.
[ 범위를 표현하는 구간 ]
- 구간 (Interval) : 두 지점 사위의 범위 -> 두 수 사이의 모든 값.
- 개구간 (Open Interval)
- 폐구간 (Closed Interval)
- 반폐구간, 반개구간 (Half-Open Interval)
[ 삼각함수의 역함수 ]
- 전단사함수로 만들어야 한다.
- 전단사함수로 만들기 위해 공역 범위를 축소하고, 치역 범위로 공역 범위를 축소한다.
- arcsin : 정의역 = [-1, 1], 공역 = [-ㅠ/2, ㅠ/2]
- arccos : 정의역 = [-1, 1], 공역 = [0, ㅠ]
- arctan : 정의역 = ㅠ/2 + nㅠ가 아닌 실수, 공역 = 실수 무한
[ 삼각함수의 역함수의 확장 - atan2 ]
- 모든 삼각함수의 역함수는 [0, 2ㅠ] 사이의 모든 값을 구할 수 없다.
ㅠ~3ㅠ/2 사이의 범위를 구하기 위해 atan2(y, x)를 만들음.
- 기존 atan과 다르게 입력값이 2개이다.
[ 단위원 (Unit Circle) ]
- 원점 (0, 0), 반지름 1인 원에 대한 직각삼각형
- 삼각함수를 이용하여 각 점의 위치를 표현하면
- a의 위치는 (cos𝜃, sin𝜃)
- b의 위치는 (cos𝜃, 0)
- c의 위치는 (0, 0)





'대학생활 > 수업' 카테고리의 다른 글
| 게임기획크리틱 4~5주차 (0) | 2023.04.12 |
|---|---|
| 게임기획크리틱 2~3주차 (0) | 2023.04.12 |
| 게임그래픽프로그래밍 4~5주차 - 좌표계, 방정식, 벡터, 내적과 외적 (0) | 2023.04.10 |
| 게임네트워크프로그래밍 4~5주차 (0) | 2023.04.10 |
| 게임네트워크프로그래밍 2~3주차 (0) | 2023.04.10 |


