6주차 - 절차적 모델링의 의미
실습 진행
- Texture가 뒤집혀서 나오는 오브젝트를 정상적으로 나오게 수정하기.
Cylinder
원통형의 모양을 가진 형태
- 원통의 높이 : height
- 원통의 반지름 : radius
- 원통의 디테일 정도 : segment
- segment 값이 클수록 원형에 근접하다.
- 정점 원통의 가장자리에 위치하며, 원의 둘레에 따라 균등하게 배치
원의 둘레에 따라서 균등하게 배치하는 방법
- 삼각 함수와 몇 등분으로 균등하게 할지는 segment의 값 이용
- radius*cosθ, radius*sinθ
Mesh 인스턴스 생성
const float PI2 = Mathf.PI * 2f; // 해당 클래스의 멤버 변수로 선언
// mesh 인스턴스 생성
var mesh = new Mesh();
// 실린더 구성 요소 준비
var vertices = new List<Vector3>();
var uvs = new List<Vector2>();
var normals = new List<Vector3>();
var triangles = new List<int>();
float height = 3f, radius = 1f;
int segments = 7;
float top = height * 0.5f, bottom = -height * 0.5f; // top과 bottom의 높이
// 측면을 구성하는 정점 데이터 생성
GenerateCap(segments + 1, top, bottom, radius, vertices, uvs, normals, true);
// 측면 삼각형을 구성하는 원 위의 정점을 참고하기 위해,
// index가 원을 한바퀴 돌기 위한 계산 -> 윈통은 위아래로 구성되어 있기 때문에
var len = (segments + 1) * 2;
// 위쪽과 아래쪽을 이어서 측면을 구성
for (int i = 0; i < segments + 1; i++)
{
int idx = i * 2;
int a = idx, b = idx + 1, c = (idx + 2), d = (idx + 3);
triangles.Add(a);
triangles.Add(c);
triangles.Add(b);
triangles.Add(d);
triangles.Add(b);
triangles.Add(c);
}원기둥의 x, y값 구하기
void GenerateCap(int segments, float top, float bottom, float radius, List<Vector3> vertices, List<Vector2> uvs, List<Vector3> normals, bool side)
{
for (int i = 0; i < segments; i++)
{
// 0.0 ~ 1.0
float ratio = (float)i / (segments - 1);
// 0.0 ~ 2π
float rad = ratio * PI2;
// 원주에 균등하게 위쪽과 아래쪽에 정점을 배치한다
float cos = Mathf.Cos(rad), sin = Mathf.Sin(rad);
float x = cos * radius, z = sin * radius; // x, z에 원주를 segment 등분한 좌표 저장
Vector3 tp = new Vector3(x, top, z), bp = new Vector3(x, bottom, z); // 위쪽, 아랫쪽 y좌표 추가
// 위쪽
vertices.Add(tp);
uvs.Add(new Vector2(ratio, 1f));
// 아래쪽
vertices.Add(bp);
uvs.Add(new Vector2(ratio, 0f));
if (side)
{
// 측면의 바깥쪽을 향하는 법선
var normal = new Vector3(cos, 0f, sin);
normals.Add(normal);
normals.Add(normal);
}
else
{
normals.Add(new Vector3(0f, 1f, 0f)); // 뚜껑의 위를 향하는 법선
normals.Add(new Vector3(0f, -1f, 0f)); // 뚜껑의 아래를 향하는 법선
}
}
}원기둥의 위 아래 뚜껑 처리
// 뚜껑의 모델을 위한 정점은 라이팅시 다른 법선을 이용하기 위해 측면과 공유하지 않고 새롭게 추가
GenerateCap(segments + 1, top, bottom, radius, vertices, uvs, normals, false);
// 위쪽 뚜껑 한가운데의 정점
vertices.Add(new Vector3(0f, top, 0f));
uvs.Add(new Vector2(0.5f, 1f));
normals.Add(new Vector3(0f, 1f, 0f));
// 아래쪽 뚜껑 한가운데의 정점
vertices.Add(new Vector3(0f, bottom, 0f)); // bottom
uvs.Add(new Vector2(0.5f, 0f));
normals.Add(new Vector3(0f, -1f, 0f));
var it = vertices.Count - 2;
var ib = vertices.Count - 1;
// 측면 정점들의 index를 참조하기 않기 위한 offset var
// GenerateCap이 두번 호출되어 vertex가 2배 들어가 있음.
var offset = len;
// 위쪽 뚜껑의 면
for (int i = 0; i < len; i += 2)
{
triangles.Add(it);
//triangles.Add((i + 2) % len + offset);
triangles.Add((i + 2) + offset);
triangles.Add(i + offset);
}
// 아래쪽 뚜껑의 면
for (int i = 1; i < len; i += 2)
{
triangles.Add(ib);
triangles.Add(i + offset);
//triangles.Add((i + 2) % len + offset);
triangles.Add((i + 2) + offset);
}최종 Mesh 인스턴스 설정
mesh.vertices = vertices.ToArray();
mesh.uv = uvs.ToArray();
mesh.normals = normals.ToArray();
mesh.triangles = triangles.ToArray();
// mesh bounding box 다시 계산
mesh.RecalculateBounds();
// mesh filter에 설정
GetComponent<MeshFilter>().mesh = mesh;Unity에서 입력값에 대한 처리
- SerializeField : 유니티가 private 데이터 멤버를 UI Inspector 창에 노출시켜서 값을 제어하고 싶을 경우 사용
- UI Inspector 창의 값을 받아서 처리하고 싶을 경우
- [Range(min, max)] : 범위의 값을 받아서 처리
public float height = 3f, radius = 1f;
public int segments = 16;
[Range(0.1f, 10f)] public float height = 3f, radius = 1f;
[Range(3, 128)] public int segments = 16;
[SerializeField, Range(0.1f, 10f)] private float height = 3f, radius = 1f;
[SerializeField, Range(3, 128)] private int segments = 16;알고리즘을 활용한 절차적 모델링 확장
식물을 만드는 데 사용되는 절차적 모델링 기법
- Unity 엔진에서는 Tree API 제공 (3D Object -> Tree)
- 식물 모델링의 대표적인 Software : Speed Tree
- 식물 생성 알고리즘의 대표주자 중 하나 : L-System
Fractal (프렉탈)
학문의 줄기. 자연계를 자세히 보면 자신의 내용을 반복적으로 복사하는 형태를 가지고 있다.
이러한 형태는 절차적인 알고리즘을 적용해서 활용 할 수 있다.
- 삼각형, 눈송이 결정, 식물 (나무), 소라와 같은 것들.
L-System
식물의 성장 프로세스에 대해서 관련 구조를 표현한 알고리즘. Fractal을 이용하여 표현한다.
물체의 한 부분을 확대했을 때 전체적인 물체의 형태가 표현되며, 나무의 가지에서 갈라진 작은 가지는 전체적인 가지의 형태와 유사하다.
- 구성요소들을 먼저 기호로 정의한다.
- 기호들을 변환하는 규칙을 정한 후 초기 상태를 시작한다.
- 규칙을 반복 적용하여 기호의 복잡도를 발전시킨다.
| 초기 문자열 : a 변환 규칙 1 : a -> ab 변환 규칙 2 : b -> a => a -> ab -> aba -> abaab -> abaababa -> abaababaabaab |
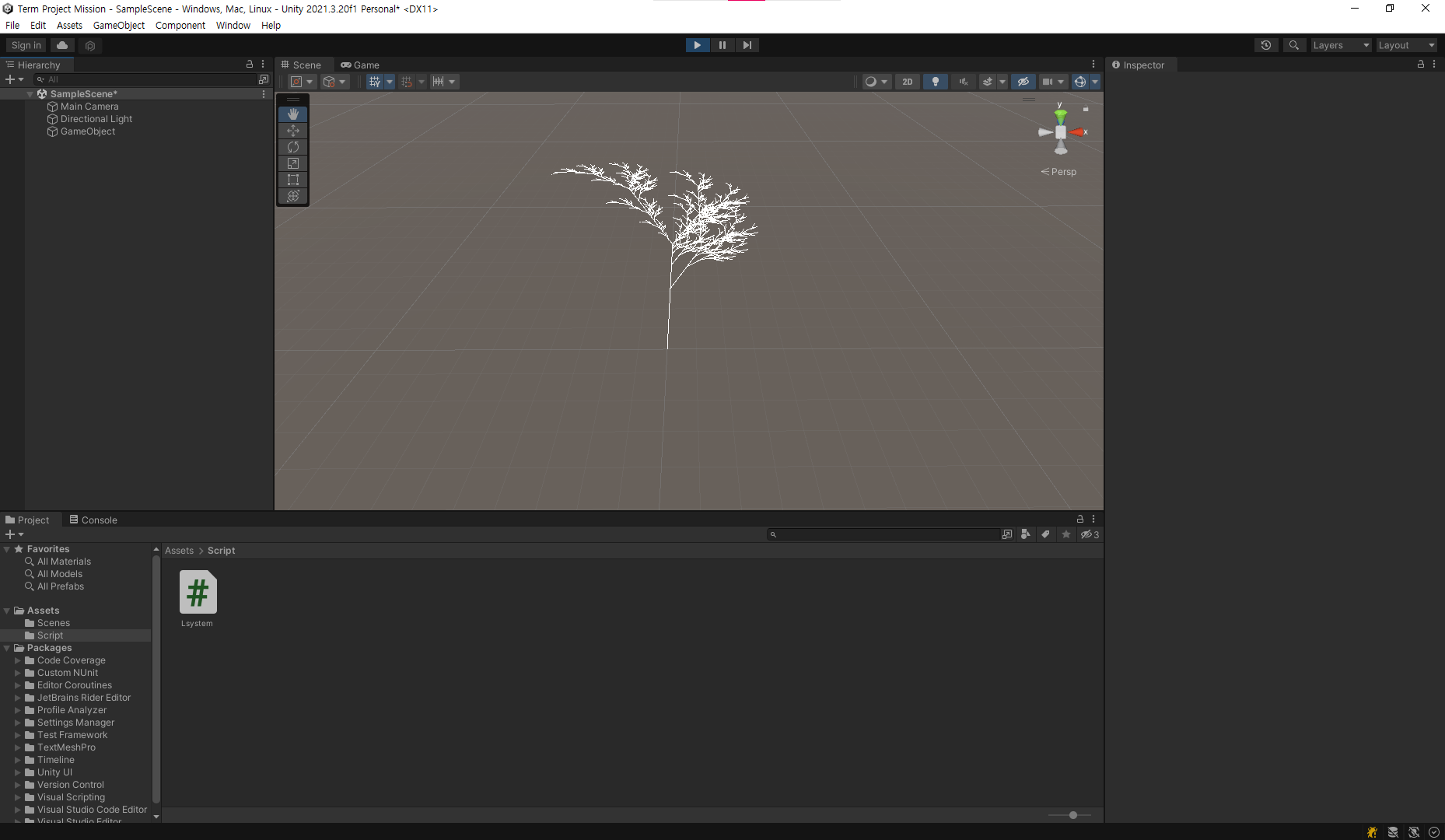
L-System을 통한 나무 그리기
나무 가지 생성, 가지 나누어짐, 다시 가지 생성하고, 가지 나누어짐.
- 나무의 분기 : 일정 각도, 좌우 방향
- 각도 : angle
- 좌, 우로 회전
- 라인 그리기
나중에 실린더를 이용하여 만드는 것을 숙제로 낼 예정.
| F : 위로 그리기 + : 오른쪽으로 Anagle만큼 회전 - : 왼쪽으로 Angle만큼 회전 [ : Stack에 현재 위치, 회전 값 저장 (push) ] : Stack에 위치, 회전 값 얻기 (pop) |
지나간 위치를 저장하는 역할을 Stack이 한다.
참고 자료 : https://en.wikipedia.org/wiki/L-system
L-system - Wikipedia
From Wikipedia, the free encyclopedia Rewriting system and type of formal grammar L-system trees form realistic models of natural patterns An L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. An L-system consists o
en.wikipedia.org
| variables : X(그리기 없음), F(위로 그리기) constants : +(오른쪽), -(왼쪽), [(push), ](pop) start variable : X rules : (X -> F + [[X]-X]-F[-FX]+X) (F -> FF) angle : 25도 axiom 선언 : 명제, 가장 기초적 근거가 되는 명제이다. 가장 처음 시작 글자 angle 값 선언 Rule에 대한 판정 처리를 위한 dictionary 대괄호에 대한 처리를 위한 stack 처리 나뭇가지 한 라인 그릴때의 길이 선언 위치값과 회전값 저장 |
실습 진행
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
struct TransformInfo
{
public Vector3 position;
public Quaternion rotation;
}
public class Lsystem : MonoBehaviour
{
//private string axiom = "A";
//private string axiom = "F";
private string axiom = "X";
private int n = 6;
private float angle;
private string currentString;
private Dictionary<char, string> rules = new Dictionary<char, string>();
private Stack<TransformInfo> transformStack = new Stack<TransformInfo>();
private bool isGenerating = false;
private float length = 0.0f;
// Start is called before the first frame update
void Start()
{
angle = 25f;
length = 10.0f;
axiom = "X";
n = 6;
rules.Add('X', "F+[[X]-X]-F[-FX]+X");
rules.Add('F', "FF");
//angle = 120f;
//length = 10.0f;
//axiom = "F-G-G";
//n = 6;
//rules.Add('F', "F-G+F+G-F");
//rules.Add('G', "GG");
currentString = axiom;
for (int genNum = 0; genNum < n; genNum++)
{
GenChar();
}
//StartCoroutine(GenerateLSystem());
DrawChar();
//DrawSierpinskiTriangle();
}
IEnumerator GenerateLSystem()
{
if (!isGenerating)
{
isGenerating = true;
StartCoroutine(Generate());
}
else
{
yield return new WaitForSeconds(0.1f);
}
}
// 규칙에 의거해서 다음 세대의 문자를 만든다.
//void Generate()
IEnumerator Generate()
{
length = length / 2f;
char[] stringChar = currentString.ToCharArray();
Debug.Log(currentString);
stringChar = currentString.ToCharArray();
for (int i = 0; i < stringChar.Length; i++)
{
char curChar = stringChar[i];
if (curChar == 'F')
{
// move forward
Vector3 initPostion = transform.position;
transform.Translate(Vector3.forward * length);
Debug.DrawLine(initPostion, transform.position, Color.white, 10000.0f, false); // duration, depthtest
yield return null;
}
else if (curChar == '+') // 회전
{
transform.Rotate(Vector3.up * angle);
}
else if (curChar == '-') // 회전
{
transform.Rotate(Vector3.up * -angle);
}
else if (curChar == '[')
{
TransformInfo ti = new TransformInfo();
ti.position = transform.position;
ti.rotation = transform.rotation;
transformStack.Push(ti);
}
else if (curChar == ']')
{
TransformInfo ti = transformStack.Pop();
transform.position = ti.position;
transform.rotation = ti.rotation;
}
}
isGenerating = false;
}
void GenChar()
{
string newString = "";
char[] stringChar = currentString.ToCharArray();
for (int i = 0; i < stringChar.Length; i++)
{
char currentChar = stringChar[i];
if (rules.ContainsKey(currentChar))
{
newString += rules[currentChar]; // A이면 AB로 B이면 A로 리턴해줌.
}
else
{
// 여기가 나오면 오류가 맞을듯.
Debug.Log("Error Converting!");
newString += currentChar.ToString();
}
}
currentString = newString;
Debug.Log(currentString);
}
void DrawChar()
{
char[] stringChar = currentString.ToCharArray();
stringChar = currentString.ToCharArray();
for (int i = 0; i < stringChar.Length; i++)
{
char curChar = stringChar[i];
if (curChar == 'F')
{
// move forward
Vector3 initPostion = transform.position;
transform.Translate(Vector3.forward * length);
Debug.DrawLine(initPostion, transform.position, Color.white, 10000.0f, false); // duration, depthtest
}
else if (curChar == '+') // 회전
{
transform.Rotate(Vector3.up * angle);
}
else if (curChar == '-') // 회전
{
transform.Rotate(Vector3.up * -angle);
}
else if (curChar == '[')
{
TransformInfo ti = new TransformInfo();
ti.position = transform.position;
ti.rotation = transform.rotation;
transformStack.Push(ti);
}
else if (curChar == ']')
{
TransformInfo ti = transformStack.Pop();
transform.position = ti.position;
transform.rotation = ti.rotation;
}
}
isGenerating = false;
}
void DrawSierpinskiTriangle()
{
char[] stringChar = currentString.ToCharArray();
stringChar = currentString.ToCharArray();
for (int i = 0; i < stringChar.Length; i++)
{
char curChar = stringChar[i];
if (curChar == 'F' || curChar == 'G')
{
// move forward
Vector3 initPostion = transform.position;
transform.Translate(Vector3.forward * length);
Debug.DrawLine(initPostion, transform.position, Color.white, 10000.0f, false); // duration, depthtest
}
else if (curChar == '+') // 회전
{
transform.Rotate(Vector3.up * angle);
}
else if (curChar == '-') // 회전
{
transform.Rotate(Vector3.up * -angle);
}
else if (curChar == '[')
{
TransformInfo ti = new TransformInfo();
ti.position = transform.position;
ti.rotation = transform.rotation;
transformStack.Push(ti);
}
else if (curChar == ']')
{
TransformInfo ti = transformStack.Pop();
transform.position = ti.position;
transform.rotation = ti.rotation;
}
}
isGenerating = false;
}
}n은 8이상 주지 않는 것이 좋다.
7주차 - 물리현상과 시뮬레이션
충돌 판정
직선(line)의 방정식
한 점과 벡터가 주어졌을 경우 직선의 방정식
- 점 P를 지나고 방향벡터 V인 직선의 방정식 : P + tV
- 두 점이 주어졌을 경우 (벡터를 구하면 됨.) : P0 + t(P1-P0)
선분(segment)의 처리
직선의 방정식을 기본으로 한다.
매개변수 t의 범위는 다음과 같이 경우에 따라 매개 변수가 정의된다.
- 두 점으로 선분을 만드는 경우 : 0 <= t <= 1
- 한 점과 벡터를 통해서 선분을 만드는 경우 : 0 <= t <= n
반직선(ray)의 처리
직선의 방정식을 기반으로 하고 있다.
한 점과 벡터를 고려한다.
- 기준점을 기반으로 해당 벡터 방향으로 무한대로 나아가는 선
- t는 0보다 크다.
게임에서 사용하는 경우
- FPS, RPG장르는 무기 특정 위치를 월드 좌표계로 변환한 후에 무기가 바라보는 벡터를 이용해서 공격을 처리한다.
- 화살 같은 탄두형 형태, 레이저건의 레이저 형태 등 형태에 따라서 충돌 처리 방식의 차이가 존재한다.
- 탄두형은 해당 방향의 벡터를 통해서 이동하고 그 객체에 대해서 충돌체크, 일반 총은 반직선이나 선분을 통해
상대방이 해당 반직선이나 선분에 충돌이 되면 피격 처리한다. 총의 사정거리가 중요하다.
평면의 방정식
한 점 P와 법선 벡터 V를 알고 있으면 평면의 방정식 계산이 가능하다.
P = (x0, y0, z0), V = (a, b, c)라고 하면
a(x - x0) + b(y - y0) + c(z - z0) = 0
ax + by + cz + d = 0
원과 구의 방정식
원과 구의 방정식의 차이는 2차원인지 3차원인지의 차이이다.
- (a, b)가 중심이고 반지름이 r인 원 : (x - a)^2 + (y - b)^2 = r^2
- (a, b, c)가 중심이고 반지름이 r인 구 : (x - a)^2 + (y - b)^2 + (z - c)^2 = r^2
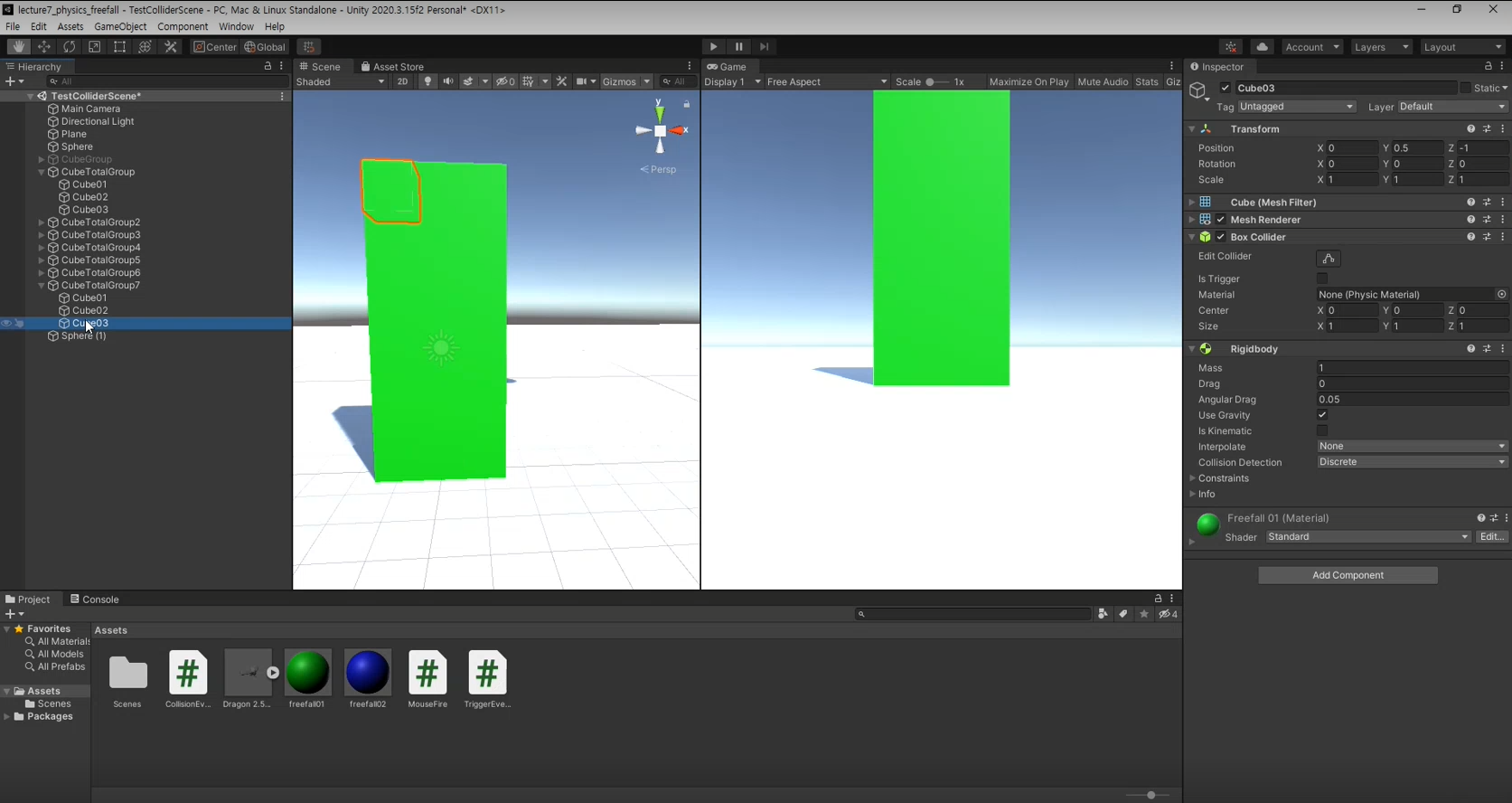
Collider (충돌체)
게임에서 사용되는 폴리곤(삼각형)은 수천, 수만 개 이상의 폴리곤을 가지고 있다.
객체들끼리의 충돌체크를 체크하기 위해서 폴리곤끼리 충돌체크를 하는 것은 비효율적이다.
객체들을 충돌 체크할 오브젝트로 처리하면 효율적이다.
- 2차원 게임에서는 원과 사각형
- 3차원 게임에서는 구와 직육면체 이용
AABB (Axis-Aligned Bounding Box)
Colider가 모든 축에 평행한 형태이다.
대부분 2D는 Bounding Box, 3D는 직육면체의 형태.
- AABB인 Box의 경우 2D, 3D 모두 매우 빠르게 충돌 체크가 가능하다.
OBB (Oriented Bounding Box)
오브젝트와 함께 회전이 가능하다.
- 충돌 계산이 AABB에 비해서 많이 복잡해진다.
- Box, Sphere, Capsule, Mesh Colider가 대표적이다.
충돌 판정
- 구와 구의 충돌 체크 : 두 원점의 거리와 반지름을 기준으로 측정 (h <= r1 + r2)
- 선분과 선분 : 두 직선의 연립 방정식을 이용하여 만나는 점이 있는지 체크 할 수 있다. 해가 존재하면 충돌 한 것.
충돌 판정 가속화
월드 상에 존재하는 모든 객체에 대해서 충돌 판정을 하면 매우 많은 연산 부하가 발생한다.
아무리 객체 하나당 원이나 구로 생각하고 계산한다고 해도, 객체가 많아지면 객체의 부하는 기하 급수적으로 증가한다.
해결을 위한 방법 1 : 범위 지정 처리
1. 특정 축을 기준으로 해서 나열 후, 그룹을 나누어서 처리하는 방법.
2. 구역을 나누어서 그 구역에 해당하는 객체들끼리 충돌 검출을 하는 방법.
해결을 위한 방법 2 : CS 형태의 게임
- 서버에서 세밀한 형태의 충돌체크는 직접 하지 못한다.
- 클라이언트에서 맵 정보와 적 정보, 객체 정보 등을 바탕으로 세밀한 충돌체크를 진행한다.
- 시간 혹은 특정 이벤트 발생시에 현재 위치를 전송한다.
- 해당 위치의 유효성을 판단한다.
- 해킹의 위험 때문에 서버에서 위치에 대한 전반적인 계산을 동시에 한 후에 클라이언트의 위치를 받았을 때의 오차 허용 범위내인지를 검증한다.
- 서버에 위치를 무조건 맡기고 처리하는 방법도 존재한다.
해결을 위한 방법 3 : 게임 종류별
- Action RPG처럼 특정 부분 판정이 디테일 하게 필요하지 않을 경우 : 원,사각형,구,직육면체 많이 사용
- Action RPG처럼, 상대에게 정확한 타격이 필요한 경우 : 각 부위별로 개별 충돌 체크 Collider 사용.
- 복잡한 형태의 객체 끼리 충돌 체크를 할 때 : Mesh Collider를 사용
- 많은 폴리곤을 가진 모델일 경우 :
1. 충돌 체크를 위한 로우 메쉬를 따로 가지고 있다가 사용.
2. 충돌 메쉬 구성 및 사용
Bullet through paper 현상
속도가 빠른 객체들이 움직이는 게임인 경우 충돌 처리 못하는 상황
- 위치 값이 많이 변하는 것들은 비용을 많이 사용하더라도 정확한 충돌 체크가 필요하다. (FPS게임에서 자주 발생한다.)
- Raycast를 이용한다.
- 게임 마다 다양한 상황이 발생 하므로, 최대한 복잡한 충돌 체크를 사용 하지 말고, 최소한의 Collider를 사용한다.
- 상세한 충돌체크가 필요한 곳에서는 Collider와 Raycast를 적절하게 혼합해서 사용해서 충돌체크 처리 필요하다.
'대학생활 > 수업' 카테고리의 다른 글
| 게임데이터설계 6~7주차 (0) | 2023.04.19 |
|---|---|
| 게임알고리즘 6주차 (0) | 2023.04.19 |
| 게임기획크리틱 6~7주차 (0) | 2023.04.18 |
| 게임그래픽프로그래밍 6~7주차 - 행렬, 선형 변환, 아핀 공간 (0) | 2023.04.17 |
| 게임네트워크프로그래밍 6~7주차 (0) | 2023.04.17 |
